En matemática, el triángulo de Pascal es una
representación de loscoeficientes binomiales ordenados en forma triangular. Es llamado así
en honor al matemático francés Blaise Pascal, quien introdujo esta notación en 1654, en
su Traité du triangle
arithmétique. Si bien las propiedades y
aplicaciones del triángulo fueron conocidas con anterioridad al tratado de
Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló
muchas de sus aplicaciones y el primero en organizar la información de manera
conjunta.
La construcción del triángulo está relacionada con
los coeficientes binomiales según la fórmula (también llamada Regla de Pascal). Si

para todo entero positivo n y todo entero
positivo k entre 0 y n.
El triángulo de Pascal se puede generalizar a dimensiones mayores. La versión de tres dimensiones se
llamapirámide de Pascal o tetraedro
de Pascal, mientras que las versiones
más generales son llamadas simplex de
Pascal.
Triángulo aritmético chino.
La primera representación explícita de un triángulo de coeficientes binomiales data del siglo X, en los comentarios de los Chandas Shastra, un libro antiguo indio de prosodia del sánscrito escrito por Pingala alrededor del año 200 a.C.
La primera representación explícita de un triángulo de coeficientes binomiales data del siglo X, en los comentarios de los Chandas Shastra, un libro antiguo indio de prosodia del sánscrito escrito por Pingala alrededor del año 200 a.C.
Las propiedades del triángulo fueron discutidas por
los matemáticos persasAl-Karaji (953–1029) y Omar Khayyám (1048–1131); de aquí que en Irán sea conocido
como el triángulo Khayyam-Pascal o simplemente el triángulo Khayyam.
Se conocían también muchos teoremas relacionados, incluyendo el teorema del binomio.
Petrus
Apianus (1495–1552) publicó el
triángulo en el frontispicio de su libro sobre cálculos comerciales Rechnung (1527). Este es el
primer registro del triángulo en Europa. En Italia, se le conoce como el triángulo de Tartaglia,
en honor al algebrista italiano Niccolò
Fontana Tartaglia(1500–77). También fue estudiado por Michael
Stifel (1486 - 1567) y François
Viète (1540-1603).
En el Traité
du triangle arithmétique (Tratado del triángulo aritmético)
publicado en 1654, Blaise Pascal reúne varios resultados ya conocidos sobre el
triángulo, y los emplea para resolver problemas ligados a la teoría de la probabilidad; demuestra 19 de sus propiedades, deducidas en
parte de la definición combinatoria de los coeficientes. Algunas de estas
propiedades eran ya conocidas y admitidas,
pero sin demostración. Para demostrarlas, Pascal pone en práctica una versión acabada de inducción matemática. Demuestra la relación entre el triángulo y la fórmula del binomio. Fue bautizado Triángulo de Pascal por Pierre Raymond de Montmort(1708) quien lo llamó: Tabla del Sr. Pascal para las combinaciones, y por Abraham de Moivre (1730) quien lo llamó: "Triangulum Arithmeticum PASCALIANUM" (del latín: "Triángulo aritmético de Pascal"), que se convirtió en el nombre occidental moderno.
pero sin demostración. Para demostrarlas, Pascal pone en práctica una versión acabada de inducción matemática. Demuestra la relación entre el triángulo y la fórmula del binomio. Fue bautizado Triángulo de Pascal por Pierre Raymond de Montmort(1708) quien lo llamó: Tabla del Sr. Pascal para las combinaciones, y por Abraham de Moivre (1730) quien lo llamó: "Triangulum Arithmeticum PASCALIANUM" (del latín: "Triángulo aritmético de Pascal"), que se convirtió en el nombre occidental moderno.

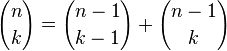

No hay comentarios.:
Publicar un comentario